Quantum-Inspired Multi-Satellite Trajectory Optimization

The next generation of space missions will rely heavily on constellations of satellites operating in coordination. Whether for planetary science, Earth observation, or defense operations, fleets of small satellites are proving to be cost-effective and resilient. They eliminate single points of failure and enable new mission concepts such as interferometry and distributed sensing.

But these opportunities bring new challenges. Controlling and optimizing the trajectories of multiple spacecraft is a problem of immense complexity. It demands robust methods that can handle high-dimensional decision spaces, nonlinear dynamics, and conflicting mission objectives—all under strict resource constraints.

Problem Formulation: Constellation Initialization

The constellation initialization problem occurs in several scenarios: immediately after launch, following catastrophic failure of one satellite, or when a mission task shifts dramatically. In each case, multiple spacecraft must move from arbitrary initial positions to a desired formation while:

• avoiding collisions,
• minimizing fuel,
• completing maneuvers in minimum time, and
• distributing resource usage fairly.

Each spacecraft is modeled as a rigid body with six degrees of freedom, actuated by on-off thrusters. The control variables are the thrust forces and torques applied during the maneuver. To keep optimization tractable, maneuvers must be represented compactly without losing generality.

Optimization-Based Strategy

Optimization-based strategies such as Genetic Algorithms (GAs), these evolutionary algorithms are inspired by natural selection and have proven effective in global search and multi-objective optimization.

Genetic Algorithm Framework

A GA begins with a population of candidate solutions, each representing a possible spacecraft trajectory. These are evaluated using a fitness function that measures their quality with respect to mission objectives. Through successive generations, solutions evolve using three operators:

• Selection – fitter solutions survive and influence the next generation.
• Recombination (crossover) – combining traits from parent solutions to create new ones.
• Mutation – introducing small random variations to maintain diversity.

Tuning a GA involves selecting parameters such as population size, crossover and mutation rates, and methods for initialization and replacement. While simple in concept, real-world implementation requires careful representation of decision variables. Compact yet general representations are essential to efficiently explore the solution space without oversimplifying the problem.

Methodology - 

Maneuver Parameterization

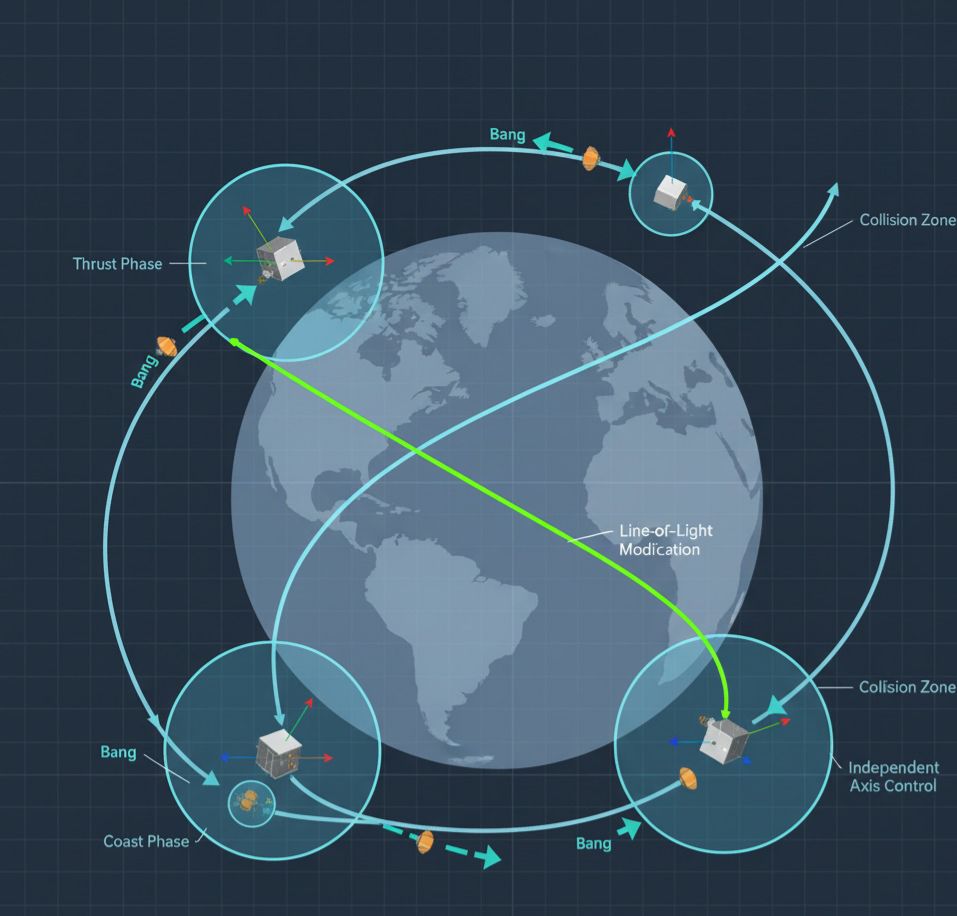
Spacecraft trajectories are often modeled using Newton/Euler six degree-of-freedom dynamics with fixed centers of mass, for instance, appropriate in small spacecraft in the 10–50 kg range. Each vehicle is assumed to have on-off thrusters (such as gas-jet RCS or PPTs) that provide discrete actuation.

For point-to-point maneuvers, spacecraft motion can be expressed using a “bang-coast-bang” control profile: a thrust phase, followed by a coast phase, and a final thrust to reach the goal.

Key assumptions include:

• Spacecraft can apply independent forces/torques along each principal axis.
• Each spacecraft has a defined spherical collision radius, simplifying collision checks.
• Trajectories are parameterized as line-of-sight (LOS) paths, with a collision avoidance (CA) component added to modify paths when needed.

This representation reduces collision detection to simple Euclidean distance checks between bounding spheres, making planning more efficient while preserving safety.

Objective Functions

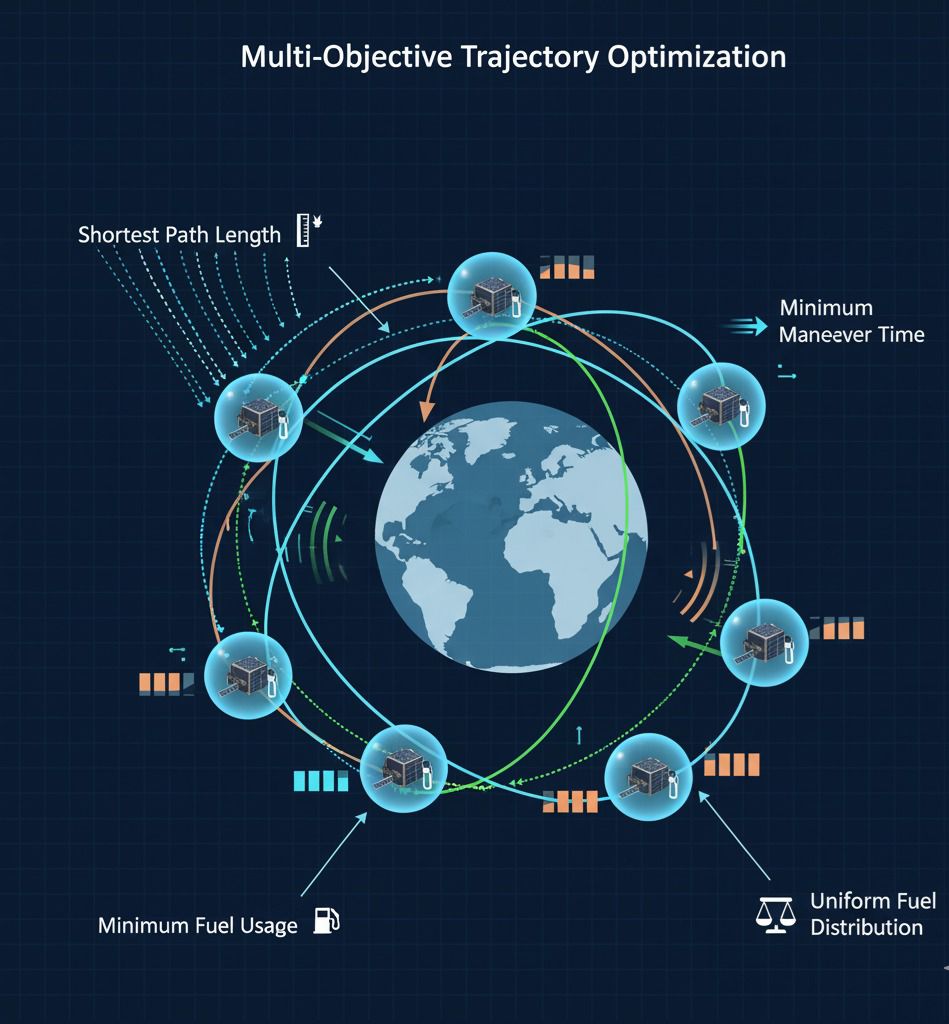
Trajectory optimization is framed as a multi-objective problem with the following criteria:

• Collision-free trajectories
• Shortest path length
• Minimum maneuver time
• Minimum fuel usage
• Uniform fuel distribution across spacecraft

The composite cost function is:

J=Jci,j+wpJp+wTTmax+wffit0−fitf+wdfitffjtflog⁡fitffjtf

Where:

• Jc (i,j): Collision Penalty for unsafe trajectories.
• Jp : Path Length Penalty, deviation from LOS.
• Tmax : Execution Time Penalty, time taken by the slowest spacecraft.
• fi (t): Fuel state of spacecraft i at time t.
• wp,wT,wf,wd: weights balancing the relative importance of each factor.

This formulation ensures that solutions are not only efficient and fast, but also safe and fair across the constellation.

Beyond Classical GAs: Quantum-Inspired Optimization (QIO)

While GAs provide a powerful global optimization framework, they often converge prematurely to local optima in highly complex problems. For satellite missions, this can translate to unsafe or suboptimal trajectories.

Quantum-Inspired Evolutionary Optimization (QIEO) extends classical GAs by enhancing the balance between exploration and exploitation. Leveraging quantum-inspired principles, QIEO explores broader regions of the solution space without sacrificing convergence speed.

BQPhy’s QIO engine shows that it outperforms classical GAs in scalability, efficiency, and mission assurance. Applied to constellation initialization and trajectory planning, QIEO consistently yields safer, faster, and more fuel-efficient solutions.

Implications for Space Missions

The integration of QIEO into satellite operations provides significant benefits:

• Maximized mission output under limited fuel and time budgets.
• Dynamic adaptability to orbital changes and live mission updates.
• Improved scheduling for high-value imaging or communication requests.
• Resilience in defense applications, such as rapid constellation deployment for drone swarm defense.

As missions become more autonomous, these methods also lay the groundwork for in-space logistics and servicing, where spacecraft can reposition or cooperate without direct ground control.

Multi-satellite trajectory optimization is among the most demanding problems in aerospace engineering. It combines nonlinear dynamics, constrained resources, and multiple conflicting objectives. While Genetic Algorithms provided the first scalable solutions, their limitations in exploration make them insufficient for increasingly complex missions.

Quantum-Inspired Evolutionary Optimization bridges this gap. By combining the evolutionary power of GAs with quantum-inspired search strategies, QIEO delivers scalable, adaptive, and high-accuracy solutions. It is poised to become a cornerstone of next-generation mission planning, from constellation initialization to autonomous orbital servicing.

FAQ's

What is Quantum-Inspired Optimization (QIO)?

QIO applies quantum-inspired principles to evolutionary algorithms, enabling faster and safer trajectory planning for multi-satellite missions.

How does QIO improve multi-satellite coordination?

It ensures collision-free trajectories while optimizing fuel usage, maneuver time, and operational fairness.

Can QIO handle complex constellations?

Yes, it scales efficiently to high-dimensional, multi-satellite dynamics that challenge classical algorithms.

Is QIO suitable for real-time mission updates?

Absolutely. QIO adapts to changing orbital conditions, satellite failures, and new mission tasks in real time.

Who benefits from QIO?

Aerospace, defense, and commercial space operators gain safer, more efficient, and scalable mission planning.

Does QIO require quantum hardware?

No, QIO runs on classical systems while leveraging quantum-inspired techniques for advanced optimization.

‍