Scaling VQLS PDE Solvers with HPC & Quantum Compilers

Block encoding is a mathematical and circuit-level technique that allows a general (non-unitary) matrix A; which might represent a physical operator, a system Hamiltonian, or a coefficient matrix—to be embedded inside a larger unitary matrix UA such that:

\( \langle 0 \rangle = \frac{A}{\alpha} \)

Here,

A is the matrix we wish to operate on (for example, a discretized differential operator),
UAis the unitary operator acting on quantum bits (which preserves probability and can be implemented on quantum hardware), and
α is a normalization constant controlling success probability.

This embedding makes it possible to execute matrix-based computations—like solving Ax=b or evolving a quantum system governed by A—using quantum hardware, where only unitaries are physically realizable.

Challenges in Scaling VQLS PDE Solvers

The challenge, however, lies in constructing UA efficiently. Inefficient implementations cause the circuit depth to grow exponentially with system size, making algorithms such as the Variational Quantum Linear Solver (VQLS) or Hamiltonian simulation impractical for realistic problems on forthcoming quantum computers (even fault-tolerant) as there is an upper limit to number of gates and decoherence time.

This research demonstrates how compiler-driven circuit synthesis using Classiq generates hardware-efficient, low-depth block encodings for structured matrices such as those arising from the 2D Poisson equation. The results show dramatic reductions in circuit depth and improved scalability, directly enhancing the feasibility of hybrid quantum algorithms on near-term hardware.

Structured Block Encoding for PDE Systems

To illustrate the use of efficient block encoding, the 2D Poisson equation is considered:

\( - \nabla^2 u = k,\; u\big|_{\partial \Omega} = 0 \)

Finite-difference discretization converts the 2D Poisson equation into a sparse linear system Au=b. In such systems, most elements of A are zero, as each grid point interacts only with nearby points.

The resulting pentadiagonal sparsity pattern enables efficient block encoding through controlled rotations and arithmetic operations, avoiding the heavy overhead of Linear Combination of Unitaries (LCU) methods.

Figure 1: 2D Poisson matrix structure and sparsity pattern

Crucially, the circuit scales logarithmically with grid size, not linearly with matrix dimensions, which a key enabler for near- and mid-term scalability.

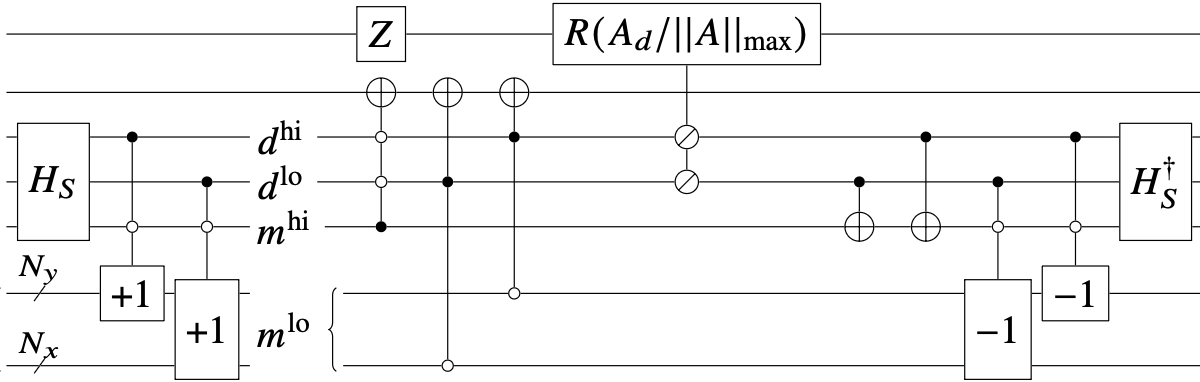
Figure 2: High-level schematic of the block encoding circuit for the discretized 2D Poisson matrix

GPU-Accelerated Simulator for Hybrid Workflow Execution

To conduct this large-scale parametric study, the benchmarks were executed on the NVIDIA CUDA-Q simulation platform.

This choice is critical because VQLS is a hybrid quantum-classical algorithm, which creates a significant development bottleneck:

Classical Bottleneck: A classical optimizer must repeatedly call the quantum circuit.
Simulation Bottleneck: Simulating that quantum circuit on a classical computer is incredibly computationally expensive.

NVIDIA CUDA-Q is a platform designed to solve this exact problem. By integrating tightly with GPU-accelerated classical HPC, it massively speeds up the quantum simulation and, just as importantly, streamlines the communication between the classical and quantum components.

This accelerated, integrated environment was essential for enabling the extensive experimentation and large-scale parametric study shown here. It allows researchers to rapidly iterate, validate complex circuits, and scale to larger problems proving an algorithm's value long before running it on scarce or noisy physical quantum hardware.

Comparing Efficient Transpilation: Classiq & Qiskit

To benchmark efficiency, identical logical block encoding circuits were implemented in:

Qiskit: Gate-level, manual control with limited global optimization.
Classiq: Compiler-based synthesis that automatically minimizes circuit depth and width.

Results:

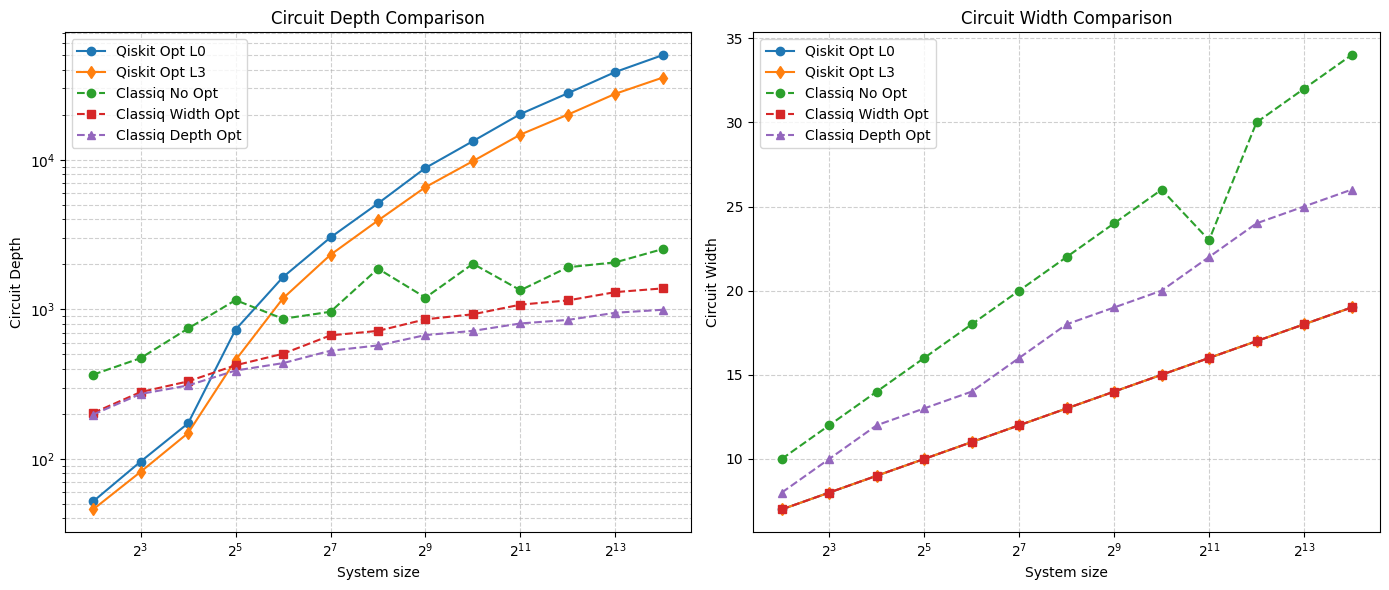
Figure 3: Comparison of post-transpilation qiskit vs classiq resources for the block encoding circuit

Depth Reduction: Classiq achieved up to 100× lower circuit depth, maintaining practical runtimes for large systems where Qiskit implementations became infeasible.
Width Trade-offs: Classiq circuits used slightly more ancilla qubits under depth-optimized settings but allowed tunable depth–width balancing.

These results show that compiler-driven synthesis can automatically identify symmetries and redundant control paths, minimize total gate count, and mitigate noise accumulation, crucial for hybrid algorithm performance.

Implications for Hybrid Quantum Algorithms (VQLS)

In Variational Quantum Linear Solvers, the encoded operator A is applied repeatedly during optimization. High circuit depth leads to accumulated noise, limiting system size and accuracy.

By reducing depth by one to two orders of magnitude, Classiq’s optimized block encodings enable:

Greater circuit fidelity under noisy conditions
Larger solvable system sizes
Improved convergence and scalability

This implementation highlights how efficient compiler-level optimization can transform theoretical algorithms into practically realizable hybrid workflows. Furthermore, platforms like NVIDIA CUDA-Q are designed to manage this exact transition, providing a single, unified programming model for today's CPU-GPU systems and tomorrow's heterogeneous CPU-GPU-QPU architectures. This approach allows algorithm teams like BQP to build and validate workflows using high-performance simulation and then seamlessly deploy the same code to physical QPU hardware, bridging the critical gap between development and execution.

Efficient block encoding is fundamental for scalable quantum computing. The comparison demonstrates that automatic synthesis using Classiq substantially outperforms manual circuit design in Qiskit, reducing depth and improving hardware viability.

Such advancements directly enhance the scalability of algorithms like VQLS and quantum PDE solvers, showing new ways for real-world quantum advantage in scientific and engineering domains.

FAQ's

‍1. What is block encoding in quantum PDE solvers?

‍Block encoding embeds a general matrix into a unitary operator, enabling quantum computation on matrices like discretized PDE operators.

2. How does Classiq optimize quantum circuits compared to Qiskit?

‍
Classiq uses compiler-driven synthesis to reduce circuit depth by up to 100× while balancing width, improving scalability and noise resilience.

3. Why is GPU acceleration important for VQLS workflows?

‍
GPU-accelerated simulators like NVIDIA CUDA-Q speed up hybrid quantum-classical optimization, enabling large-scale parametric studies efficiently.

4. What are the advantages of efficient block encoding for VQLS?

‍
It allows larger system sizes, higher fidelity under noisy conditions, faster convergence, and practical scalability for hybrid algorithms.

5. Can these workflows run on actual quantum hardware?

‍
Yes, optimized block encodings and hybrid workflows can be directly deployed on quantum hardware after high-performance simulation validation.