Quantum-Inspired Optimization for Engineers

Engineering problems are becoming more complex. Design spaces with thousands of variables, multiple objectives, and nonlinear constraints can push traditional optimization methods to their limits. 

Classical solvers often get stuck in local optima or require long computation times.

Quantum-inspired optimization (QIO) offers a practical approach. It applies principles inspired by quantum mechanics on standard computers, allowing engineers to explore many design options at once, escape local traps, and reach near-optimal solutions faster.

The global quantum-inspired optimization AI market was valued at $1.2 billion in 2024 and is forecasted to reach $14.7 billion by 2033, growing at 32.5% annually. 

In this blog, we cover how QIO works, the core principles behind it, common methods engineers use, and real-world use cases across aerospace, energy, and structural engineering. 

We also look at how platforms like BQP integrate quantum-inspired optimization into existing workflows to make complex design exploration faster and more manageable.

What Is Quantum-Inspired Optimization?

Quantum-inspired optimization uses ideas from quantum mechanics to improve how classical computers solve optimization problems. It does not require quantum hardware. Instead, it applies quantum principles like superposition and tunneling through algorithms that run on standard CPUs and GPUs.

Classical optimization methods work sequentially, testing one solution at a time or following gradients toward nearby optima. QIO explores multiple solution paths simultaneously, mimics quantum tunneling to escape local traps, and models correlations between design variables more effectively.

For engineers, this means:

• Faster exploration of large design spaces with thousands of variables.
• Better solutions by avoiding local minima that trap classical methods.
• Practical implementation using existing hardware and workflows.

Engineering problems like minimizing satellite weight, optimizing energy distribution in power grids, or balancing cost and performance in structural designs benefit directly from QIO's ability to handle complexity and find near-global optima efficiently.

What are the Core Principles of Quantum-Inspired Optimization?

QIO draws from three quantum mechanics concepts and translates them into practical algorithms that run on classical systems.

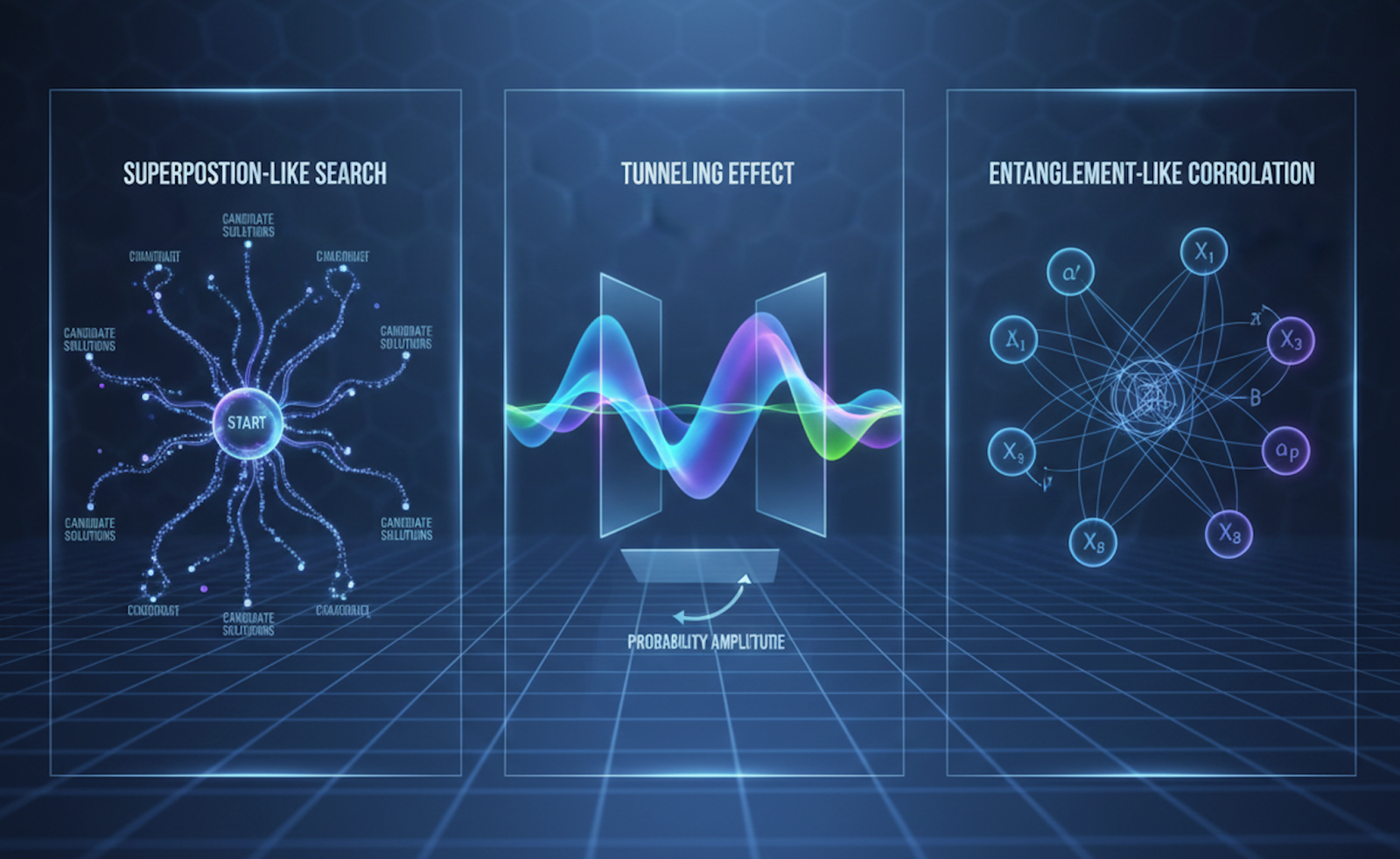
1. Superposition-Like Search

Quantum-inspired optimization lets engineers explore many design options at the same time instead of testing one after another.

It works like running multiple “what if” scenarios at once. Instead of changing one parameter, checking the result, and moving to the next, it evaluates several combinations together.

This approach helps find good solutions faster, especially for complex problems with lots of variables where testing options one by one would take too long.

2. Tunneling Emulation

Quantum tunneling allows particles to pass through barriers they normally couldn’t. In optimization, this helps escape local minima.

Traditional methods can get stuck in solutions that look good but aren’t the best overall.

Tunneling lets the solver jump out of these traps and keep searching for better options.

It’s particularly useful for complex problems with many peaks and valleys, like topology optimization or aerodynamic designs with multiple targets.

3. Entanglement-Like Correlation

In real engineering systems, variables rarely act alone. Changing a wing’s shape affects lift and drag. Material choice impacts weight, cost, and thermal performance.

Entanglement-like correlation lets the solver consider these relationships together instead of separately.

This leads to designs that are more balanced and perform well across multiple objectives at once.

How QIO Works in Practical Engineering Problems?

Implementing quantum-inspired optimization follows a straightforward process that integrates with existing engineering workflows.

Step 1: Map the Problem

Convert design goals into a mathematical optimization model. This includes defining:

• Objective functions (what to minimize or maximize).
• Design variables (parameters you can adjust).
• Constraints (limits that must be satisfied).

Many QIO methods reformulate problems into QUBO (Quadratic Unconstrained Binary Optimization) format, a mathematical structure well-suited for quantum-inspired solving. Engineers don't need to handle this conversion manually modern platforms automate the reformulation.

Step 2: Run the QIO Solver

The quantum-inspired algorithm explores the solution space using the principles described above. It generates candidate solutions, evaluates them against objectives and constraints, and iteratively refines the search toward optimal regions.

This happens on standard hardware CPUs, GPUs, or HPC clusters. No specialized quantum processors required.

Step 3: Review and Select Solutions

QIO solvers return a set of high-performing designs, often including Pareto-optimal solutions for multi-objective problems. Engineers evaluate these candidates, consider trade-offs, and select designs for detailed validation through simulation or testing.

The process integrates with MATLAB, Python, or engineering-specific solvers. Teams can embed QIO into existing CAD-to-simulation pipelines without rebuilding workflows from scratch.

What are the Common QIO Methods Engineers Use ?

Several quantum-inspired techniques have emerged, each suited to different problem types and engineering contexts.

1. Quantum-Inspired Particle Swarm Optimization (QIPS)

Standard Particle Swarm Optimization (PSO) mimics social behavior in bird flocks, where individuals search for solutions while sharing information about promising regions.

QIPS enhances this by incorporating quantum-style position updates. Particles explore the design space with greater diversity, reducing the risk of premature convergence to local optima.

Best for: Continuous optimization problems with smooth but multimodal objective functions.

2. Quantum-Inspired Genetic Algorithms

Genetic algorithms evolve populations of solutions through selection, crossover, and mutation. Quantum-inspired variants use quantum bit representations (qubits) to encode candidate solutions.

This increases population diversity and allows the algorithm to explore broader regions of the design space simultaneously. The result is faster convergence and better final solutions compared to classical genetic algorithms.

Best for: Combinatorial problems, discrete optimization, and scenarios requiring robust global search.

3. QUBO-Based Digital Annealing

QUBO formulations express optimization problems as binary quadratic models. Digital annealing solvers use simulated quantum tunneling effects to find optimal binary variable assignments.

These methods run on classical hardware but mimic the behavior of quantum annealers, delivering up to 20× faster solutions for complex design and scheduling problems compared to traditional methods.

Best for: Scheduling, resource allocation, configuration optimization, and graph-based problems.

4. Variational and Hybrid QIO Variants

Hybrid approaches combine classical optimization techniques with quantum-inspired layers. For example, a solver might use gradient-based methods for continuous variables while applying QIO techniques to discrete or combinatorial aspects of the same problem.

This balance delivers both speed and precision, leveraging the strengths of each approach where they perform best.

Best for: Mixed-integer problems, multi-stage optimization, and large-scale systems with both continuous and discrete variables.

For more on how these methods apply to aerospace and defense challenges, see our guide on quantum-inspired optimization in aerospace and defense.

Engineering Use Cases for QIO

Quantum-inspired optimization addresses real engineering challenges across multiple industries.

1.Aerospace

Mission planning and trajectory optimization involve balancing fuel use, time limits, and safety across thousands of possible paths. QIO explores these options quickly, helping engineers find near-optimal flight paths for satellites or UAVs.

Lightweight structural design also benefits. QIO can handle complex topology problems, finding configurations that improve strength-to-weight ratios solutions that traditional methods might miss.

2.Structural and Civil Engineering

QIO helps engineers figure out how forces travel through structures and where reinforcements are needed. It balances cost, safety, and material use efficiently.

Stiffness analysis and compliance optimization for bridges, buildings, and machinery improve because QIO can explore unconventional material arrangements that maximize performance within limits.

3.Energy Systems

Managing power grids requires quick decisions to balance supply and demand. QIO handles complex switching and resource allocation faster than traditional methods.

Renewable energy planning, such as deciding which sources to use, where to store energy, and how to route power, also benefits from QIO’s ability to consider multiple variables at once.

All these cases share common traits: large design spaces, multiple competing goals, and time-sensitive decisions. QIO reduces iteration cycles, saves costs, and delivers faster, better solutions.

Common Engineering Tools and Frameworks for QIO

Quantum-inspired optimization is accessible through tools that integrate with standard engineering workflows.

1.QUBO Solvers and Digital Annealers

These run on CPUs and GPUs without specialized quantum hardware. They accept problem formulations in standard formats and return optimized solutions using quantum-inspired search techniques.

2.Integration with MATLAB and Python

Most QIO libraries provide APIs for MATLAB and Python, allowing engineers to call quantum-inspired solvers from familiar scripting environments. This makes it easy to embed QIO into existing design automation pipelines.

3.Compatibility with CAD, FEA, and Simulation Tools

QIO doesn't replace simulation tools, it enhances them. Engineers continue using ANSYS, Abaqus, STAR-CCM+, or other domain-specific software while QIO handles the optimization layer on top.

No special hardware, no quantum physics expertise, and no workflow disruption. QIO fits into the tools engineers already use.

How BQP Supports Quantum-Inspired Optimization?

BQP brings quantum-inspired optimization directly into engineering simulation workflows, eliminating the fragmentation between optimization and analysis.

The platform unifies quantum-inspired search within BQP's simulation framework, so engineers define objectives, constraints, and variables in one interface:

• Quantum-inspired solvers built-in – No need to license separate optimization software or write custom scripts.
• Automated problem setup – Define goals and constraints; BQP handles the mathematical reformulation.
• Real-time performance tracking – Monitor convergence, compare quantum-inspired runs against classical methods, and adjust parameters on the fly.
• Hybrid quantum-classical integration – Plug quantum-inspired algorithms into existing HPC and GPU workflows without system overhauls.
• Industry-specific templates – Pre-configured workflows for aerospace, defense, and energy applications reduce setup time.

With BQP, tasks that used to take many rounds of trial and error now complete much faster. Engineers can explore more design options while the platform handles the complexity, letting them focus on making better design decisions.

Learn more about how simulation and optimization work together in our article on simulation-driven optimization in digital mission engineering.

Try quantum-inspired optimization with BQP. Book a Demo.

Conclusion

Quantum-inspired optimization delivers quantum-level efficiency on classical hardware. Engineers gain faster convergence, better escape from local optima, and the ability to handle larger, more complex design spaces without waiting for quantum computers to mature.

The technology is practical, accessible, and ready for adoption today. It integrates with existing tools, runs on standard infrastructure, and produces measurable improvements in optimization speed and solution quality.

As engineering problems grow more complex and competitive pressures increase, teams that adopt quantum-inspired methods early will have a clear advantage in design efficiency and innovation speed. For more insights on where the field is heading, explore our article on the future of aerospace with quantum-inspired simulation.

Boost your optimization workflow with BQP's quantum-inspired tools. Book a Demo.

FAQs

1. What is quantum-inspired optimization?

Quantum-inspired optimization applies principles from quantum mechanics like superposition and tunneling to classical computers. It helps engineers solve complex optimization problems faster without needing quantum hardware.

2. Do I need quantum computers to use quantum-inspired optimization?

No. Quantum-inspired optimization runs on standard CPUs, GPUs, and HPC systems. It borrows ideas from quantum mechanics but does not require quantum processors.

3. How does quantum-inspired optimization differ from classical methods?

Classical methods explore solutions sequentially or follow gradients. Quantum-inspired methods explore multiple paths simultaneously, escape local optima more effectively, and model variable correlations better, leading to faster convergence and better solutions.

4. What types of engineering problems benefit most from QIO?

Problems with large design spaces, many local optima, combinatorial complexity, or multi-objective trade-offs benefit most. Examples include trajectory optimization, topology optimization, scheduling, and resource allocation.

5. Can quantum-inspired optimization integrate with existing engineering tools?

Yes. QIO integrates with MATLAB, Python, CAD, FEA, and simulation platforms. Engineers can embed QIO into existing workflows without replacing tools or rebuilding processes.