Optimizing UAV Mission Coordination

The deployment of cooperative teams of unmanned aerial vehicles (UAVs) has redefined the mission planning process across defense and aerospace applications. Missions such as suppression of enemy air defenses, reconnaissance, and coordinated strikes require precise timing and synchronization between autonomous aerial agents. The capability of a coordinated fleet far exceeds the sum of its individual parts, but achieving this cooperation introduces extreme computational complexity.

Modern missions demand algorithms that can scale dynamically from conceptual planning to real-time execution under uncertainty, constraints, and minimal tolerance for error. This is the focus of Coordinated Target Assignment and Path Planning (CTAPP), a foundational problem in multi-UAV autonomy.

Problem Definition

The CTAPP problem involves two interlinked objectives:

1. Assign UAVs to targets optimally.
2. Generate flyable, feasible, and safe flight paths that satisfy timing constraints.

The core optimization problem can be expressed as:

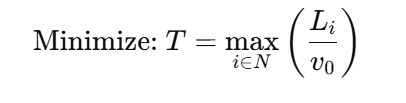
where:

• Li  is the total length of the flight path for UAV iii,
• v0  is the nominal cruise velocity, and
• T is the total mission time (defined by the longest flight path).

The objective is to minimize T, ensuring all UAVs arrive simultaneously or sequentially at their assigned targets.

Each UAV i must be assigned to one target j, subject to the constraints:

This assignment forms the Linear Bottleneck Assignment Problem (LBAP), where the goal is to minimize the maximum path cost rather than the sum of all costs.

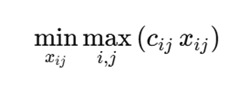
Here, c_ij  denotes the cost associated with UAV i flying to target j, usually represented by the computed path length or fuel cost.

Phase 1 – Individual Path Generation

Each UAV computes the shortest feasible path to every potential target using a network-based approach. The operational area is discretized into a graph of possible flight corridors. Crossing paths are connected via clothoids and circular arcs, ensuring smooth transitions that satisfy UAV acceleration limits.

Let each edge e_kl  of the network represent a segment between vertices k and l, with an associated cost equal to its length d_kl . The total path length for UAV i to target j is then:

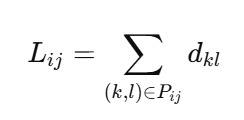
where P_ij  is the sequence of connected edges forming the shortest feasible path.
For example, the Dijkstra or A* algorithm is applied to identify the minimum-cost path under the constraints:

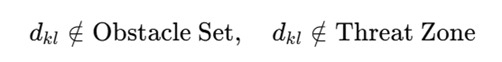
All paths generated satisfy flyability (respecting vehicle kinematics) and feasibility (avoiding restricted regions).

Phase 2 – Target Assignment

After all feasible paths are generated, UAVs are optimally assigned to targets. The goal is to minimize the maximum path cost, thereby reducing total mission time:

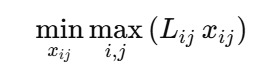
This formulation—known as the Linear Bottleneck Assignment Problem (LBAP)—can be efficiently solved using the threshold algorithm with computational complexity O(n^2.5/log n).

The output yields:

• Assignment Matrix X=[x_ij], identifying the UAV–target pairings, and
• Critical Path Length L_max =max(L_ij x_ij ), representing the longest (reference) path.

The mission duration is then:

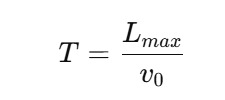
Phase 3 – Flight Path Adaptation and Coordination

For synchronized missions, shorter paths must be prolonged or timed to match the critical path duration T.
 This is achieved using waypoint insertion and velocity adaptation techniques.

Each candidate waypoint ppp introduces an alternative path L(p) defined as:

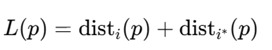
where:

• dist_i (p) = distance from UAV i’s start to waypoint p,
• dist_i∗(p) = distance from waypoint p to assigned target i^∗.

A waypoint p is viable if:

The UAV’s adjusted velocity along path L(p) becomes:

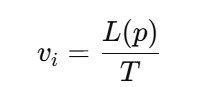
To ensure safety, inter-UAV separation is checked continuously:

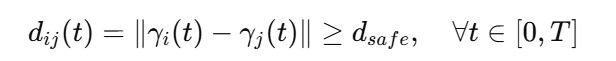
where γ_i (t) and γ_j (t) denote the position vectors of UAVs i and j at time t.

Sequential Arrival Missions

For sequential or multi-phase missions, UAVs must arrive at the same target with predefined time delays Δt_i.
Flight times are adjusted as:

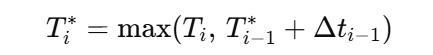
and total mission time becomes:

T_total =T_n^∗  

Paths are then modified via waypoint insertion or minor curvature adjustments to match T_i^∗  for each UAV while maintaining safety and feasibility.

Performance and Computational Challenges

While the described approach is robust, classical optimization techniques face scalability issues as the number of UAVs, targets, and constraints increase. The combinatorial explosion of possible assignments and paths leads to exponential computational cost. Real-time adaptation under dynamic threats or moving targets is especially challenging using traditional deterministic or heuristic solvers.

Quantum-Inspired Optimization for CTAPP

To address these challenges, Quantum-Inspired Evolutionary Optimization (QIEO) provides a paradigm shift. While running on classical hardware, QIEO uses quantum probability amplitudes to maintain population diversity and perform parallel search across the solution space.

Key advantages include:

1. Exploration: Parallel probabilistic encoding prevents convergence to local optima.
2. Speed: Faster convergence toward global solutions supports near real-time re-planning.
3. Scalability: Handles large-scale, multi-agent coordination problems efficiently.
4. Adaptability: Integrates live mission data for on-the-fly optimization adjustments.

When applied to CTAPP, QIEO can simultaneously optimize target assignment and trajectory generation while preserving feasibility and timing constraints — a capability unattainable by classical heuristics alone.

Coordinated Target Assignment in UAV Path Planning missions present a comprehensive framework for multi-UAV mission coordination under timing, safety, and operational constraints. By integrating graph-based path generation, bottleneck assignment optimization, and adaptive coordination strategies, it provides a strong foundation for mission-critical autonomy.

However, classical methods remain bounded by computational limitations. Quantum-Inspired Optimization offers a scalable and efficient alternative — bridging the gap between real-time adaptability and computational feasibility. For future aerospace and defense missions, this hybrid approach represents a decisive advancement toward precision, reliability, and autonomy in coordinated air operations.