Hybrid Quantum–Classical CFD with VQLS

Computational Fluid Dynamics (CFD) is central to aerospace and defense design. High-fidelity simulations support design, certification, and digital-twin workflows. But full-fidelity CFD often exceeds available compute and time budgets.

BQP’s Hybrid Quantum–Classical Method (HQCM) approach expands the possibility for large scale CFD simulation that is future ready with current computing systems.  This research has showed how Variational Quantum Linear Solvers (VQLS) can be made practical for CFD. 

Limitations in Traditional CFD

High-fidelity methods such as wall-resolved LES and DNS give accurate physics. It also require enormous memory and compute time.  This makes them impractical for routine design cycles across the whole flight envelope.

Discretization of PDEs in CFD yields large linear systems. These systems grow quickly with grid refinement and with 3D physics. Classical solvers (CG, GMRES, multigrid) hit scaling and turnaround limits for many industrial cases.

BQP’s CFD Approach

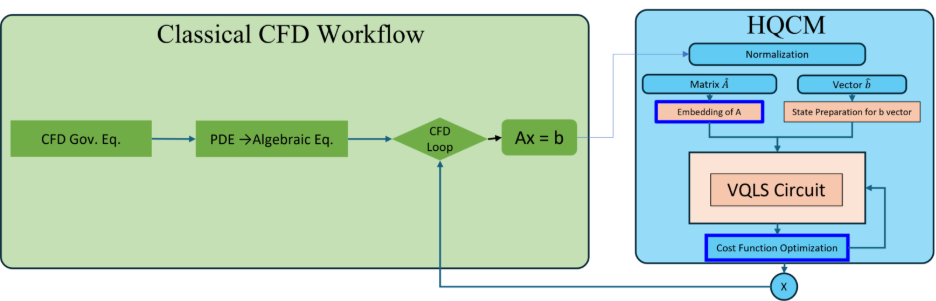
Figure 1: BQP’s HQCM framework

Quantum algorithms target linear-algebra kernels directly. Variational Quantum Linear Solvers (VQLS) recast linear solver as a parameter optimization problem by combining it with Quantum Inspired Evolutionary Optimization (QIEO) algorithms. This makes VQLS attractive for the pressure–Poisson and diffusion solves common in CFD.

Hybrid quantum–classical work flows can fit into existing CFD pipelines. Near-term (NISQ) devices cannot run deep, fault-tolerant algorithms. But carefully designed hybrid methods can reduce the overall cost of the linear solve step. 

Problem and Challenge Addressed

Two practical bottlenecks limit VQLS for CFD. First, matrix decomposition into Pauli terms often produces an exponentially large number of terms. That increases circuit counts, measurement overhead, and time.

Second, variational optimization can stall because of barren plateaus. Vanishing gradients slow or stop training as the number of parameters or system size grows. This work targets both issues with oracle-based block encoding and a quantum-inspired evolutionary optimizer.

Methodology

BQP’s HQCM workflow starts from a standard CFD discretization and hands the linear solve to a VQLS circuit.

Discretize the PDE (finite difference, finite element, or finite volume) to obtain: Ax=b, where ACNN, x is unknown vector and b the right hand side. 

Overview of VQLS (equations and cost)

VQLS represents A as a linear combination of unitaries: A=clAl, with clCand unitaries Al.

The variational ansatz prepares the state |x()=V()|0n^, with n=log2⁡N.

The algorithm minimizes the cost C=1−|b,|2, ∣Ψ(θ)⟩= A∣x(θ)⟩ / [⟨x(θ)∣A†A∣x(θ)⟩]^1/2 

Evaluating C directly with naive Pauli decompositions requires OL2 Hadamard tests and many circuits. 

That cost becomes prohibitive for CFD matrices where L can grow quickly. 

Oracle-based block encoding

Block encoding embeds a scaled non-unitary A into a larger unitary U_A:

‍

‍

and satisfies, for some >0  and error A−0m,INUA,0mIN2

Here m is the number of ancilla qubits used for the embedding. When U_A acts on |0m^|x  and ancillas are post-selected in |0m^ , the principal register is projected approximately onto  . The success probability is P_success =∥A∣x⟩∥²/(∣α∣2)

For structured sparse matrices (tridiagonal/pentadiagonal), oracle-based constructions implement U_A with circuits whose width and depth scale polynomially in log₂N.

This reduces the number of distinct circuit evaluations required to estimate the terms in C( ). 

Practical block encoding details

For a tridiagonal matrix with sparsity s=3, round up to the next power of two and set k= log₂s.

The block-encoding unitary U_A then acts on n+k+1 qubits (system + ancillas). In practice, oracle construction uses arithmetic unitaries (left/right shift) and small controlled rotations. The ancilla count stays constant with N for fixed sparsity, which helps scalability.

Discretization and benchmark problems (equations)

1D Poisson (Dirichlet):

−d2udx2=k,u0=u1=0

Central finite-difference discretization yields a symmetric tridiagonal matrix

‍

which is scaled by its spectral radius to satisfy ||A||2 1. 

2D Poisson (Dirichlet):−2ux2+2uy2=k

On a uniform grid the system matrix is a Kronecker sum:A=IT+TNyI with each T_N the 1D Laplacian matrix shown above divided by x2. The pentadiagonal structure has maximum sparsity s = 5 and similarly admits an oracle-based embedding.

Ansatz, measurement and cost evaluation

BQP uses a hardware-efficient ansatz built from single-qubit Ry rotations and CZ entangling layers on alternating neighbor pairs.

 By combining the oracle-based U_A with the ansatz, the full VQLS cost can be estimated from a single (deeper) circuit plus post-selection and sufficient measurement shots. The block-encoding approach moves measurement overhead from many different circuits to one circuit with more shots.

Optimization: QIEO vs COBYLA

COBYLA is a popular gradient-free optimizer. It performs well on small systems but struggles as problem size grows. Barren plateaus appear and gradients vanish, causing slow or stalled convergence.

Quantum-Inspired Evolutionary Optimizer (QIEO) is a meta-huristic population-based method. It explores parameters broadly and recovers from flat regions. QIEO is also amenable to GPU-accelerated parallel implementation. 

The HQCM method was evaluated on the 1D and 2D Poisson problems and on a 2D steady-state heat conduction case.

 Key quantitative outcomes follow.

• Oracle-based block encoding reduced circuit depth and circuit count relative to LCU-style decompositions.
• VQLS with QIEO avoided barren-plateau induced stalls up to 32×3232\times32 matrix tests.
• Quantum-assisted solutions matched classical results for the heat conduction diagonal profiles within numerical tolerance.

Additional numerical details. Oracle-based constructions deliver circuit depth and width that scale as poly(log₂N).

Measurement strategy. The single-circuit block-encoded VQLS recovers the overlap |b','|2 by post-selection:

‍

where m is the number of ancillas used in the block encoding. Sufficient measurement shots on one circuit yield the statistical estimates needed to compute C( ).

Implications

This HQCM approach has practical implications for aerospace and defense simulation pipelines. It offers a near-term bridge between classical HPC and future fault-tolerant quantum systems.

For design cycles, accelerating the linear solve reduces wall-clock time for implicit solvers. Faster solves enable more configurations per design iteration and richer parametric studies. This is particularly relevant for pressure-Poisson steps in incompressible Navier–Stokes solvers.

For digital twins and operational analytics, the ability to run higher-fidelity updates more frequently improves model fidelity. This supports condition-based maintenance and scenario analysis for defense platforms.

From an operational standpoint, offloading the most expensive linear algebra kernels to quantum-assisted solvers can reduce HPC run time and energy consumption. That said, near-term deployment requires careful engineering: error mitigation, measurement-shot planning, and hybrid orchestration must be part of the integration plan.

The HQCM framework mitigates two primary obstacles to practical VQLS for CFD: circuit count/depth and barren-plateau optimization failure. Oracle-based block encoding reduces circuit multiplicity and measurement overhead.

QIEO stabilizes optimization at larger problem sizes. Together these advances point to a realistic, incremental path for quantum-assisted CFD in aerospace and defense.