Trajectory Optimization for Missiles Using a Multitier Approach

Optimizing missile trajectories is a complex problem that directly impacts mission success. Classical optimization methods face significant challenges when addressing long-range intercepts, multi-phase guidance, and stochastic uncertainties inherent in missile flight. A multitier approach to trajectory design offers a structured solution, improving guidance performance across both midcourse and terminal phases.

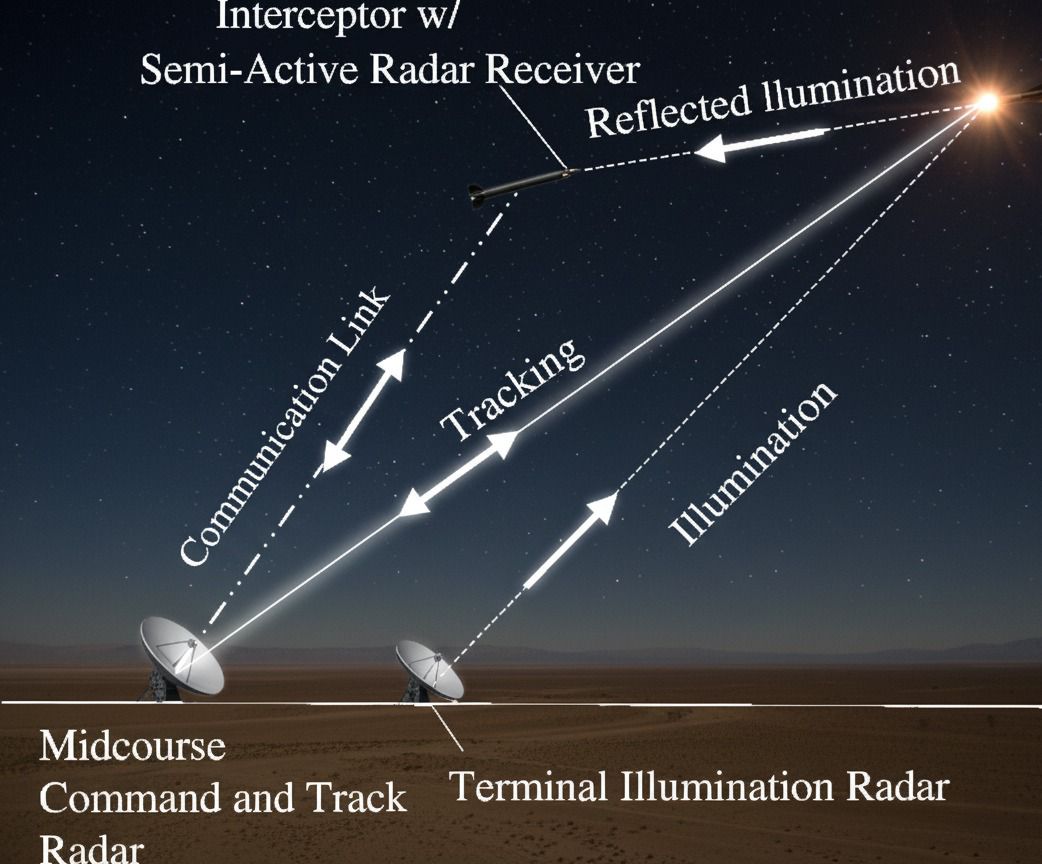
Missiles often operate through multiple guidance phases, each relying on different sensors and control laws. A two-tier trajectory design approach separates the mission into:

• First-tier (midcourse phase): Optimizes the missile’s flight path to reach a handover state suitable for terminal guidance.
• Second-tier (terminal homing phase): Uses onboard sensors to finalize intercept, accounting for stochastic noise and target maneuvers.

The first tier incorporates an auxiliary approach angle constraint at handover, which governs the field of optimal midcourse trajectories. The second-tier model estimates the probability of hit using Monte Carlo simulations, incorporating seeker noise, missile instrument errors, and target maneuvering.

Challenges in Classical Optimization

Trajectory optimization in defense applications faces several complexities:

• Handover sensitivity: The transition from midcourse to terminal guidance must satisfy precise conditions to maximize probability of hit.
• Stochastic uncertainties: Target maneuvers, sensor noise, and missile airframe dynamics introduce non-deterministic errors.
• Nonlinear constraints: Flight dynamics and energy management create highly nonlinear optimization landscapes.
• Computational cost: Monte Carlo simulations for probability of hit estimation are expensive when paired with classical trajectory optimizers.

Classical methods such as proportional navigation or standard optimal control may converge prematurely or fail to explore the full solution space.

Methodology: Two-Tier Optimization

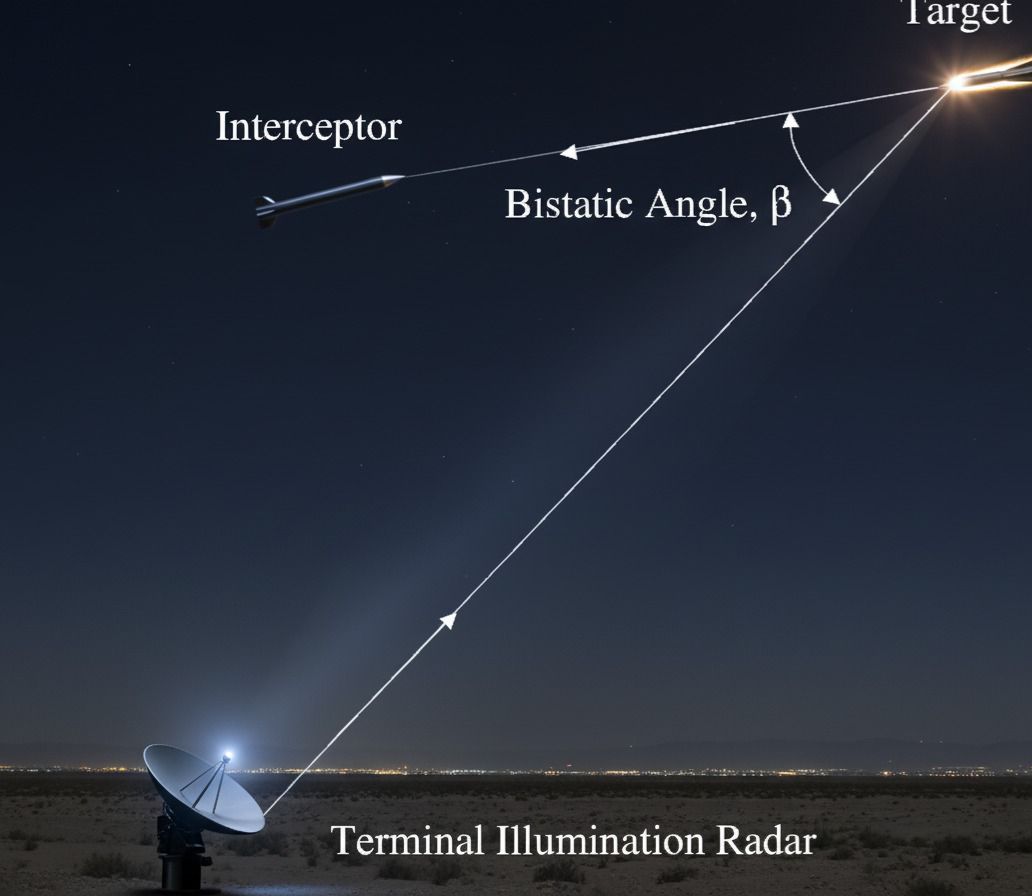
First-Tier Dynamics

The first-tier model employs a two-degree-of-freedom point-mass model over a single plane with spherical Earth approximation. It is governed by the following equations:

Where (x) and (z) are position states in the inertial frame, (V) is velocity, and (\gamma) is the flight-path angle.

The optimizer selects:

• Flight-path angle at the end of the first stage I.
• Control history and handover time tho to maximize missile energy at handover.
• Approach angle constraint approach               for defining optimal trajectory fields.

Second-Tier Dynamics

The terminal homing phase is modeled with similar planar dynamics, initialized using handover states from the first tier:

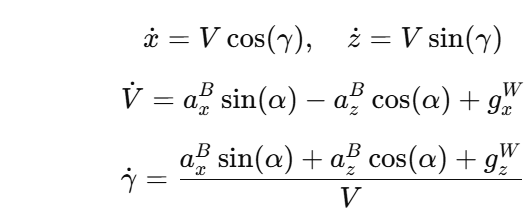
Where axB,azB are the measured boresight error and   is the angle of attack, and gxW,gzW are gravitational components.

The seeker dynamics are approximated as a first-order lag:

hs˙=emeasSs

Where emeas is the measured boresight error and ss  is the seeker time constant. Noise sources are added to simulate real-world conditions:

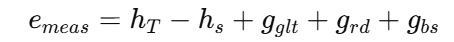
Probability of Hit

Monte Carlo simulations compute the probability of hit (P_{hit}) for each approach angle:

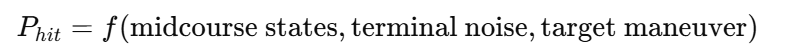
The optimal approach angle maximizes P_(hit), ensuring the best overall trajectory for the multitier guidance system.

Why Quantum-Inspired Optimization?

Classical methods struggle with combinatorial, nonlinear, and stochastic aspects of multitier missile guidance. Quantum-Inspired Optimization (QIO) offers:

• Efficient exploration of large, nonlinear solution spaces.
• Natural incorporation of stochastic uncertainties.
• Reduced computational time with improved global optimality.

A platform like BQPhy allows exploration of solutions using QIO for complex missile trajectory optimization and other defense applications.

Try BQPhy’s free trial to experience the potential of quantum-inspired optimization in trajectory design.

FAQ'S

What is multitier trajectory optimization?

It separates missile flight into midcourse and terminal phases, optimizing each to maximize guidance accuracy and hit probability.

Why do classical methods struggle with missile trajectories?

Classical algorithms face nonlinear constraints, stochastic uncertainties, and high computational costs that limit optimal solutions.

How does QIO improve missile guidance?

QIO explores larger solution spaces efficiently, accounts for stochastic effects, and achieves better global optimality for complex trajectories.

Can QIO handle real-world uncertainties?

Yes, it naturally incorporates stochastic noise, target maneuvers, and sensor errors into trajectory optimization.

Who benefits from QIO-based trajectory optimization?

Defense organizations, aerospace engineers, and missile system developers gain improved guidance accuracy and mission success.

Does QIO require quantum hardware?

No, QIO runs on classical hardware while using quantum-inspired principles to enhance optimization performance.