Quantum-Inspired Multi-Phase Missile Trajectories

The terminal trajectory of an anti-ship missile is a multi-phase, multi-objective optimization problem. Each phase imposes unique aerodynamic, control, and time constraints, making optimization a highly complex task. Traditional algorithms like GA and PSO have been applied, but they struggle with scalability and real-time performance.

Quantum-inspired optimization (QIO) provides a methodological breakthrough, enabling better handling of constraints, real-time updates, and large-dimensional search spaces.

Multi-Phase Terminal Trajectory Model

The missile’s trajectory is divided into seven phases, each with distinct dynamics:

1. Cruise Phase – fixed altitude, maximum speed, line-of-sight alignment.
   
   1. Governed by proportional-derivative (PD) feedback laws.
   2. State equation (simplified form):

xm˙=Vcoscos,y˙m=Vcossin,zm˙=Vsin

2. Ascent Phase – rapid climb for superior detection capability.
3. Tracking Phase – radar seeker activated, guidance based on azimuth and elevation:

'=+,'=+

4. Descent Phase – rapid drop to sea-skimming altitude to evade radar.
5. Stabilization Phase – low-altitude, constant-speed approach.
6. Pre-Dive Phase – steep ascent for terminal dive setup.
7. Dive Phase – terminal vertical dive using proportional navigation law:

Design Variables

The optimization problem involves tuning key parameters across phases:

• Altitude thresholds 
• Distance thresholds 
• Control coefficients 

Final optimization vector:

X=R5,R6,K2,,K11

resulting in a 12-dimensional optimization space.

Optimization Objective

The goal is to minimize miss distance while maximizing terminal impact angle:

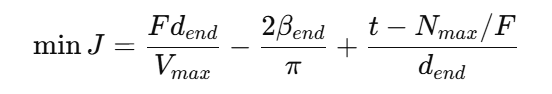
Subject to constraints:

end<0,VVmax,pmendR

This multi-objective function intertwines accuracy, impact posture, and time efficiency, requiring sophisticated optimization methods.

Classical Methods vs. Quantum-Inspired Optimization

Classical Algorithms (GA, PSO, ACO)

‍Genetic algorithms, particle swarm optimization, and ant colony optimization have been used extensively for missile trajectory problems. While they provide effective global search capabilities, they often suffer from premature convergence and face scalability issues. As the dimensionality of the problem increases, their performance degrades significantly, making them less reliable for real-time, high-complexity defense scenarios.

Hybrid Multi-Objective Particle Swarm Optimization -

The MOPSO-h variant was developed to overcome some of these challenges by combining particle swarm optimization with adaptive mutation strategies. This allows a better balance between global exploration and local refinement. Simulation studies have shown strong results, such as reducing the mean miss distance to within 2.34 meters and maintaining a terminal impact angle above 85°. However, these improvements come at the cost of computational efficiency, limiting their practical use in rapidly changing combat environments.

Quantum-Inspired Evolutionary Optimization (QIEO)

‍QIEO introduces optimization strategies derived from quantum principles, implemented on classical hardware. It maintains solution diversity through quantum probability amplitudes, preventing premature convergence and ensuring broader search coverage. At the same time, it accelerates convergence in high-dimensional search spaces, allowing complex, multi-phase trajectory problems to be optimized far more efficiently than classical methods.

Why Quantum-Inspired is Better

‍ QIEO provides four critical advantages. In exploration, it evaluates multiple solutions simultaneously, avoiding local optima. In speed, it converges more rapidly, supporting near real-time decision-making. In scalability, it handles the growing dimensionality of multi-phase problems without exponential slowdowns. Finally, in adaptability, it integrates live seeker data and responds dynamically to evasive maneuvers or countermeasures, ensuring optimization remains effective under operational pressures.

FAQ's

How complex are anti-ship missile trajectories?

Multi-phase trajectories involve seven distinct flight phases, each with unique dynamics and constraints.

Why do classical methods struggle?

Classical algorithms like GA and PSO often converge prematurely, face scalability issues, and are slower in real-time applications.

How does QIEO improve optimization?

Quantum-Inspired Evolutionary Optimization maintains solution diversity, accelerates convergence, and handles high-dimensional search spaces efficiently.

Can QIO adapt to live operational data?

Yes, QIO integrates live seeker data and responds dynamically to evasive maneuvers or countermeasures.

What are the key benefits of using QIO?

Faster, scalable, and adaptive multi-phase optimization ensures higher accuracy, improved penetration effectiveness, and operational reliability.