Missile Defense Shield Design: Quantum-Inspired Optimization

Modern missile defense systems must respond to threats that evolve in speed, maneuverability, and unpredictability. Traditional algorithms have supported guidance and interception for decades, but as operational environments grow more complex, their limitations become increasingly clear.

Key challenges include:

• Dynamic engagement conditions where targets may alter trajectory mid-flight.
• Acceleration and control limits that restrict missile maneuverability.
• Uncertainty in prediction of incoming missile paths under adversarial maneuvers.

These conditions make guidance optimization a multidimensional problem where classical methods often converge to suboptimal solutions.

Classical Methods and Limitations

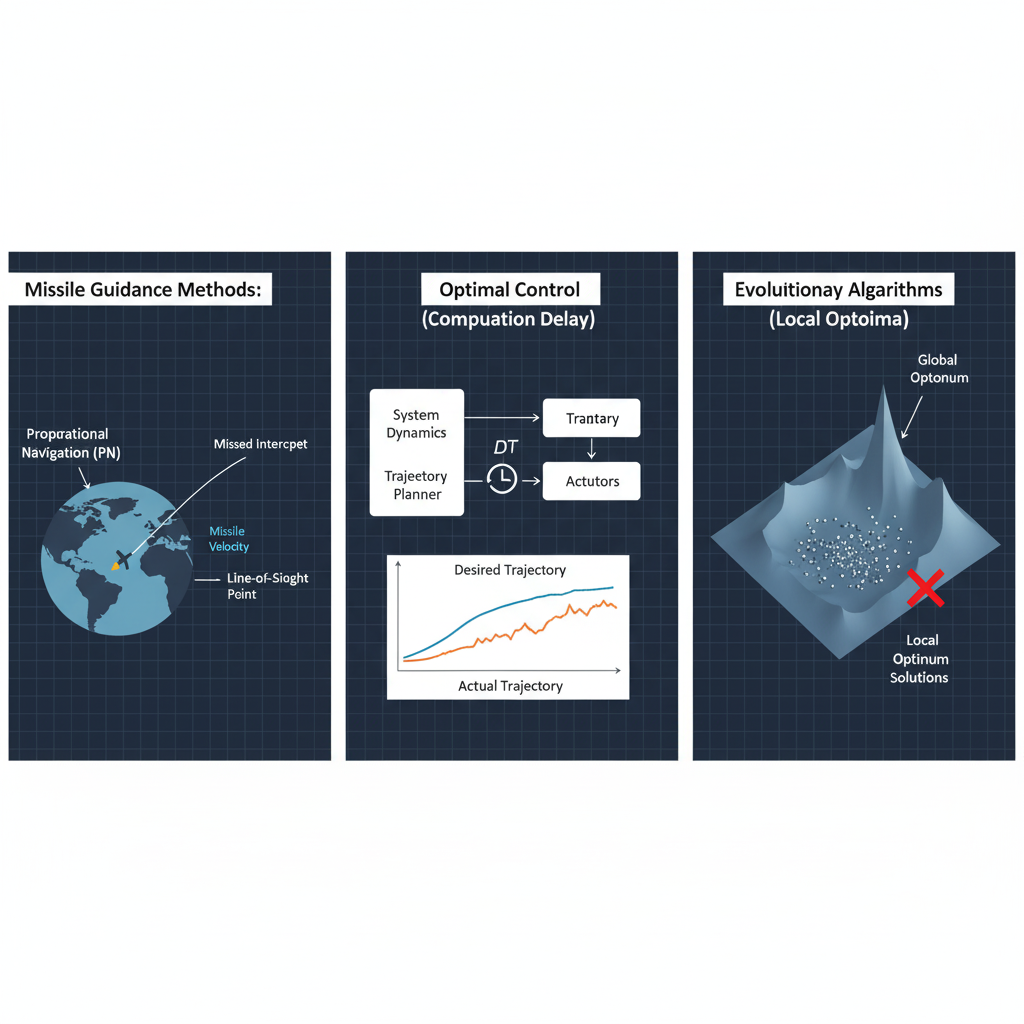
Missile guidance has historically relied on proportional navigation (PN) and optimal control methods.

• Proportional Navigation (PN): Relies on target position and velocity but does not account for evasive maneuvers. It risks premature convergence and limited adaptability.
• Optimal Control Guidance: Uses system dynamics models but is computationally intensive and less effective for real-time adaptation in high-dimensional environments.
• Genetic and Evolutionary Algorithms: Provide heuristic optimization but often face slow convergence, difficulty scaling, and poor constraint handling in multidimensional defense problems.

These methods can yield feasible results but fall short when required to guarantee global optimality under real-world operational constraints.

Methodology: Modeling and Optimization

A missile’s dynamics are represented using reference frames and transformation matrices. For instance, the transformation from wind frame to inertial frame is expressed as:

Missile acceleration in the wind frame is given by:

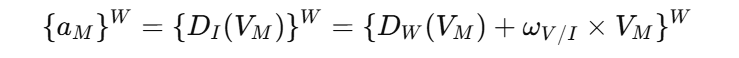
Resulting in:

˙    

The system dynamics are modeled as nonlinear discrete equations:

xˉk+1=Fkxˉk,uˉk,yˉk=hxˉk

with the cost function for optimal control:

Juˉ1,uˉ2,,uˉN−1=12uˉkTRkuˉk  

This framework captures realistic missile aerodynamics, thrust variability, and autopilot dynamics under acceleration constraints. However, solving such problems to global optimality within real-time windows is where classical algorithms struggle.

3. Why Quantum-Inspired Optimization?

Quantum-inspired optimization (QIO) addresses these challenges by mimicking quantum principles on classical hardware. Instead of converging prematurely to local minima, QIO algorithms evaluate multiple candidate solutions simultaneously across vast search spaces.

Advantages include:

• Broader search exploration: Avoids local optima through quantum-inspired sampling.
• Faster convergence: Achieves real-time decision-making essential for interception.
• Scalability: Handles high-dimensional optimization problems at operational scale.
• Constraint adaptability: Incorporates acceleration, trajectory, and timing constraints without significant computational penalties.

In missile defense, this translates into:

• More accurate prediction of incoming missile positions.
• Improved interception success rates under adversarial maneuvers.
• Better utilization of missile energy and control authority.

By enabling global optimization, quantum-inspired methods improve not just computational efficiency but also the accuracy and reliability of life-critical defense decisions.

Real-World Readiness

Quantum-inspired approaches do not require quantum hardware, making them deployable today. They can be integrated into mission planning and adaptive interception systems, ensuring defense networks remain responsive under rapidly evolving threats.

Explore BQPhy’s Free Trial

To help defense, aerospace, and space organizations explore these methods, BQPhy offers a free trial program. This initiative enables teams to test quantum-inspired optimization on their own mission-critical challenges, from missile defense to swarm coordination and beyond.

FAQs

Why do classical guidance methods struggle?

‍Classical methods often converge to suboptimal solutions and cannot adapt quickly in real-time.

How does quantum-inspired optimization help?

‍It evaluates multiple solutions simultaneously, achieving faster and more accurate threat predictions.

Can QIO run on classical hardware?

‍Yes, QIO works on standard systems without requiring quantum computers.

What operational benefits does QIO provide?

‍It improves interception success rates and optimizes missile energy usage.‍

Is QIO suitable for real-time defense scenarios?

‍Yes, it enables rapid decision-making under changing threat conditions.